Shapiro –Wilk Test
What is the Shapiro-Wilk Test?
The Shapiro-Wilk test is a statistical test that evaluates the normality of a population. It was developed by Samuel Sanford Shapiro and Martin Wilk in 1965.
Basically, this test uses a null hypothesis that states that the sample comes from a normally distributed population. Thus, if the p-value obtained is greater than the chosen alpha level, this null hypothesis cannot be rejected. Conversely, if the p-value is lower than the chosen alpha level, this null hypothesis is rejected, showing evidence that the data under study is not normally distributed.
The test statistic used is:
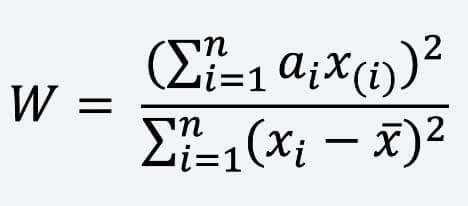
Where is th-smallest number in the sample (called the th order statistic), is the sample mean, and xi are the ordered sample values. The constants ai are obtained from the covariances, variances, and means of n random variables sampled from the standard normal distribution. The limit values for this test statistic are estimated by using Monte-Carlo simulations
This test presents some bias related to the sample size. Thus, the larger the sample, the higher the likelihood that the sample will be considered normally distributed.
Why is the Shapiro-Wilk Test Important?
Knowing whether a population is normally distributed or not is very important in research and engineering, as this fact provides the base for deciding which statistical methods to use.
The consequences also extend to model construction, because once it is known that the data is normally distributed, most of the necessary statistical constructs become available from statistical theory.
Shapiro-Wilk Test + LogicPlum
Applying the Shapiro-Wilk test requires a sound knowledge of the mathematics inside the method. Not all model creation practitioners have this knowledge, and therefore, they are constrained in their analysis and modeling of datasets.
However, they usually have knowledge and experience in their areas of work, such as finance, economics, and engineering. LogicPlum blends both areas of expertise by automating all mathematical and statistical calculations. In this way, its users can concentrate on interpreting the model and forecasting future events, knowing that they are using the best machine learning technologies available.
Guide to Further Reading
Wikipedia. (2020). Shapiro-Wilk Test. Available at https://en.wikipedia.org/wiki/Shapiro%E2%80%93Wilk_test








