What is the Expected Value?
The Expected Value of a random variable X is the arithmetic mean of many independent outcomes of X. In statistics, it’s denoted as E[X] or E(X), and its formal definition is:
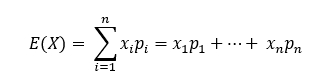
Where xi and pi are different outcomes of X and their respective probabilities, and n represents the total number of outcomes.
Note: this formula is valid when n is a finite number.
This concept originated in the 17th century from the “problem of points.” In their proposed solutions, French mathematicians Blaise Pascal and Pierre de Fermat suggested the principle that the value of a future gain is directly proportional to the probability of getting it. Years later, Dutch mathematician Christiaan Huygens showed how to calculate the expected value in general cases. Pierre-Simon Laplace formalized this concept in 1814.
Why Is The Expected Value Important?
The expected value is a core concept of statistics and probability theory. In probability theory, it’s also called the mean, average, first moment, or expectation; it is used to calculate the variance of a distribution.
In neural networks, expected values are part of many training algorithms and can be calculated using Mixture Density Networks (MDNs).
This concept is widely employed in sciences and engineering. For example, in finance, it represents the anticipated value of an investment at a specific future time. In this manner, by calculating the expected values of different alternatives, investors can choose the best options for them.
In classical mechanics, this concept appears in the center of the mass calculation, and in quantum mechanics is fundamental to calculate uncertainty.
In biology and genetics, the concept of expected value is central to most experiments and tests, similarly, in chemistry and economics.
Expected Value and LogicPlum
LogicPlum’s foundations develop from statistics and artificial intelligence. As such, the concept of expected value is embedded in this platform. It applies it not only to perform statistical tests but also in the many algorithms used to calculate correlations and do classifications.
Additional Resources
- Tanton, J.(2005) Encyclopedia of Mathematics. Facts on file. NY.








