What Is The Probability Density Function?

The probability density function (PDF) or density of a random variable is the relationship between the outcomes and their probabilities. It can be used to calculate the likelihood that the random variable value is within a given range. The whole shape of this function is referred to as a probability distribution.

Formally:

For a continuous random variable X with an absolutely continuous, differentiable cumulative distribution function (CDF) F_X(x), the probability density function f_X(x) is defined by

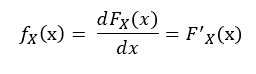
For a discrete random variable:

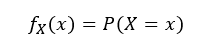
The probability density function is generally attributed to Simpson, who mentioned it in his 1757 response to Bayes’s critique of his 1755 letter on de Moivre’s theory of errors.

It is not uncommon that the probability density function of a sample is unknown. One way to estimate it is by using a process known as the probability density estimation based on the construction of a histogram of values.

Why Is The Probability Density Function Valuable?

The probability density function is one of the fundamental constructs in statistics. It can help calculate the moments of a distribution, such as the mean and variance, and determine which sample values can be considered outliers.

It is also used in analytics to determine which methods can be used or not, as some algorithms require specific probability distributions.

The applications are legion. For example, it may be used in finance to calculate the probability that a stock price increases within a range, for example, 3 – 5 %. In Quantum Mechanics, they are used to describe systems’ behavior, and in Chemical Engineering, probability density functions are used to solve the problem of turbulent mixing with chemical reactions.

Probability Density Function and LogicPlum

Probability density functions are at the heart of Statistics, and thus, of LogicPlum’s platform. This system provides ways to estimate it and uses these functions to select training algorithms.

Once the platform has trained several algorithms, probability distributions and probability density functions are considered for error calculation.

Additional Resources

• Khan Academy. Probability Density Functions. Available athttps://www.khanacademy.org/math/statistics-probability/random-variables-stats-library/random-variables-continuous/v/probability-density-functions