What are the Sigmoid Functions?

Sigmoid functions are a class of functions that present an S type of shape. The best-known examples are the logistic function and the tanh. Below is a list of the most typical ones:

Logistic function:

Hyperbolic tangent:

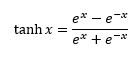
Arctangent:

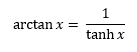
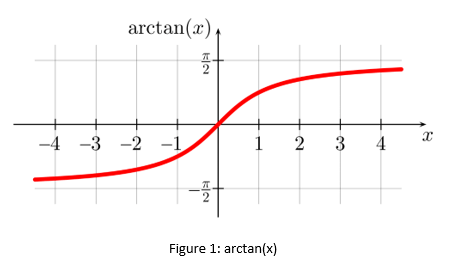
Figure 1: arctan(x)

Gudermannian function:

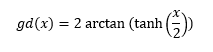
Error function:

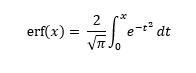
Why is the Sigmoid Function Valuable?

Sigmoid functions are widely used in science and engineering when necessary to simulate processes that present a slow initial growth, followed by rapid development, and having a limited value at the end.

In agricultural science, they are used to model the crop yield as a function of both water and water salinity. In biochemistry and pharmacology, the Hill equation and Hill–Langmuir equation follow a sigmoid pattern. And, in audio, they are used to simulate the sound of an analog circuitry clipping.

As the growth behavior presented by this family of functions has the advantage of permitting some control over the growth process, these functions are frequently used in control theory when a feature needs to vary between a minimum and a maximum value.

For similar reasons, in computer graphics, sigmoid functions are used to blend different colors. In machine learning, they are applied in various roles, such as activation functions and error calculations.

Sigmoid Functions and LogicPlum

LogicPlum’s automated approach to machine learning allows users to create models without the need for in-depth mathematical knowledge or complicated calculations. Thus, many models can be tried (each containing different sigmoid functions) and the optimal one chosen.

This automation also means that LogicPlum’s platform can generate detailed technical reports about the modeling process, which can be easily analyzed by experts and non-experts alike.

As a result, all stakeholders can participate in model creation, contributing to their specific areas of knowledge.

Additional Resources

• Sharma, S. (2017). Activation Functions in Neural Networks.