What is a Gaussian Function?

In mathematics, a Gaussian function is a function of the following form:

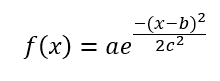
Where a,b, and c are real value constants, c > 0, and

a: is the height of the curve’s peak,

b: is the position of the center of the peak, and

c: defines the width of the “bell”.

This family of functions is named after German mathematician Carl Friedrich Gauss. It is characterized by the symmetric “bell curve shape”.

Gaussian functions are used to represent the probability density function of a normally distributed random variable, where b is the expected value (μ) and c the variance (σ). The resulting function is:

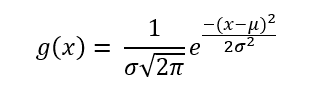
Why are Gaussian Functions Important?

Gaussian functions appear in many areas of science and engineering. In statistics and probability theory, they are used as the density function of a normal distribution. In Physics, they appear in the quantum harmonic oscillator, quantum field theory, optics, lasers, and many other theories and models.

Similarly, in chemistry they are used to represent molecular orbitals; and in computer science, Gaussian functions are used in vision systems and image processing. In artificial intelligence, they are used to define some types of neural networks.

Its applicability also extends to engineering where it is used to model financial scenarios, chemical processes, nuclear reactions, and more.

Gaussian Functions and LogicPlum

Gaussian functions are one of the most important tools in modeling, where they are used to represent probabilities, generate neural networks, and verify experimental results among other uses. As such they are an integral part of LogicPlum’s platform.

The main advantage of this platform is its approach to machine learning-based modeling. Through automation, it allows its users to test and evaluate hundreds of different models and select the most efficient one without the need for them to be experts in statistics or programming. In addition, it produces automatically generated reports that describe the modeling process in depth.

As a result, users can contribute within their fields of expertise, such as finance, engineering, and medicine; knowing that their models include the most advanced mathematical and computational technologies.

Additional Resources

• Wikipedia. (2020). Gaussian function. Available at https://en.wikipedia.org/wiki/Gaussian_function